10万人の母集団に対して、信頼度を95%とし誤差を5%許容する前提だと、必要サンプル数は約380人と計算できます。
同じ信頼度で誤差を3%とすると、必要サンプル数は約1,000人と計算できます。
このように統計サンプルの数を論理的に決めるときに役立つのが、「統計サンプル数を決める数式」です。
この記事では、統計の基礎的手法であるサンプリング数の取り方と、統計データの階級の取り方を紹介していきます。
以下のような人におすすめの記事になっています。
- アンケート調査をするにあたって、適切なサンプリング数を知りたい
- 統計データのきれいにまとめる方法を知りたい
統計サンプル数の決め方は?決めるための数式
統計サンプル数を求めるのに役立つのが、以下に示した「サンプル数を決定するための計算式」です。
n = N / [ (ε/μ(α))2 × {(N-1)/ρ(1-ρ)} + 1 ]
n : 必要サンプル数
μ(α) : 信頼度100-αのときの正規分布の値、信頼度が高いほど高くなる。
通常は信頼度95%の1.96か、信頼度99%の2.58を使います。
N : 調査したい母集団の大きさ
ε : 精度(誤差)
ρ : 母比率(これは経験的に求めるか、最もnが大きくなる0.5を用います)
この式は、必要とする信頼度と精度によって、サンプル数が異なることを示します。
ある集団の傾向を掴むときに、その集団の数があまりに膨大だと、すべてを調査することは不可能です。
たとえば、10万人の集団の傾向を掴むためだからといって、10万人全員を調査することはできません。
そうすると、母集団の中からサンプルをいくつか抽出して、全体の傾向を分析する(サンプリング調査をする)のが一般的です。
しかし、10万人の集団に対してサンプル数が10人だと、いくらなんでもサンプル数が少なすぎると感じることでしょう。
そこで役に立つのが、上記の式なのです。
統計サンプル数を決めるのは母集団の大きさ、信頼度、精度
精度の誤差0%を目指すなら、εは0になるので、数式は以下のようになります。
n = N / [ 0 + 1 ] = N
つまり必要サンプル数nは、母集団と同じNになります。
数式によると、調査の信頼度μ(α)を大きくしても、必要サンプル数が大きくなるとわかります。
統計サンプル数の計算事例
10万人の町で、ある調査を実施する場合のサンプル数nを考えてみましょう。
このとき、信頼度を95%とすると、μ(α)=1.96 と、精度εには上下5%となる0.05を,ρ=0.5を採用するとします。
その場合、必要サンプル数は、次のように計算できます。
n = 100000 / [(0.05/1.96)2 × {(99999)/0.25)} + 1 ] = 383人
μ(α) : 信頼度95%で1.96
N : 調査したい母集団の大きさ 100,000人
ε : 精度(誤差) 5%
ρ : 母比率0.5
つまり、母集団10万人の傾向を調査するには、上下5%の誤差範囲で、95%の確からしさを許容するなら、400人の調査で十分なのです。
統計の妥当なサンプル数は?
母集団が100万人や1000万人であっても、統計上は400人も調査をすれば十分に信頼に足るデータが集められます。
なぜなら、統計学上で有意水準されているのは、サンプルの誤差が5%以下とされているからです。
もう一度先ほどの計算式で計算してみましょう。
誤差5%、信頼性95%のまま母集団の数を変化させると、必要サンプル数は以下のように計算できます。
| 母集団 | 1000人 | 1万人 | 10万人 | 100万人 | 1000万人 |
| サンプル数 | 278人 | 379人 | 383人 | 384人 | 384人 |
条件
μ(α) : 信頼度95%で1.96
ε : 精度(誤差) 5%
ρ : 母比率0.5
この結果から、母集団1万人であっても、1000万人であっても、母集団の傾向を誤差5%、95%の確からしさで調査する場合、400人程度の調査をすれば十分だということがわかります。
※あくまでサンプリングの偏りがないことが前提になります。
さらに、信頼性を高めるために誤差3%で考えると、以下のとおりです。
| 母集団 | 1000人 | 1万人 | 10万人 | 100万人 | 1000万人 |
| サンプル数 | 516人 | 964人 | 1056人 | 1065人 | 1067人 |
条件
μ(α) : 信頼度95%で1.96
ε : 精度(誤差) 3%
ρ : 母比率0.5
10万人以上の母集団に対して3%の精度で統計をとるなら、1000人くらいで十分だということです。
このことから考えると、人口1000万人弱の東京都を母集団とした調査の場合、500人から1,000人程度のサンプリングとしておけば十分に信頼に足る統計データになるといえるのです。
度数分布表における最適な数値範囲と階級の数
あるデータを、範囲ごとに区切って傾向を見たい場合には、度数分布表(ヒストグラム)を用います。
度数分布表とは、以下のように、ある範囲の数字が、どのくらいの数存在しているのかを示したグラフです。
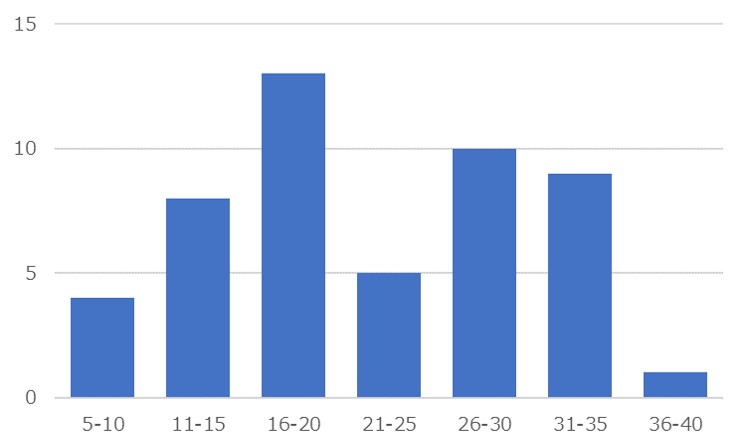
この度数分布表を作るときに、考えるべきことがデータの範囲と階級、つまり数字をいくつで区切るか?ということです。
たとえば、次の50個のデータを度数分布表にすることを考えます。
| 7 | 8 | 10 | 10 | 11 | 12 | 12 | 13 |
| 15 | 15 | 15 | 15 | 16 | 16 | 16 | 17 |
| 17 | 18 | 18 | 18 | 18 | 19 | 19 | 20 |
| 20 | 21 | 22 | 23 | 23 | 24 | 26 | 26 |
| 27 | 28 | 29 | 29 | 29 | 29 | 30 | 30 |
| 31 | 31 | 31 | 32 | 33 | 35 | 35 | 35 |
| 35 | 39 |
このデータを適切な範囲と階級に分けるとき、どのようにすればよいでしょうか。
たとえば、直感的に5刻みで分けると次のように7つの階級に分けられます。(ちなみに、5刻みにしたのが、上記のグラフです)
| 範囲 | 度数 |
| 5~10 | 4 |
| 11~15 | 8 |
| 16~20 | 13 |
| 21~25 | 5 |
| 26~30 | 10 |
| 31~35 | 9 |
| 36~40 | 1 |
ここで、階級数を粗くしすぎると全体感がぼやけてしまいますし、細かすぎると度数分布にする意味がなくなってしまうので、適切な範囲と階級で分ける必要があります。
そこで適切な範囲と階級を求める公式であるスタージェスの公式を使います。
スタージェスの公式を使うことで、次のように最適な範囲Cと階級Kを求められます。
範囲C = (サンプル最大値-サンプル最小値)/(1+log2(サンプル数))
階級K = 1 + log2(サンプル数)
先ほどの例で、スタージェスの公式を使うと範囲Cと階級Kは以下のようになります。
範囲C = 4.82
階級K = 6.64
つまり、範囲は4~5で刻み、階級は6~7にするのがよいということです。
スタージェスの公式を使うことで、大雑把に分けた範囲5と階級7で問題ないことが確認できました。
このように、スタージェスの公式を使うことで、度数分布表の範囲と階級を明確にできるのです。
まとめ
以上、アンケートなどで使うサンプリング数の決め方と、度数分布表における数値範囲と階級数の決め方でした。
- 統計に必要となるサンプル数は数、式によって決められる。
- 信頼度95%、誤差3%を許容した場合、1,000人強のサンプルがあれば、母集団1000万人の統計としても有効に機能する。(誤差5%まで許容すれば400人でも問題ない)
- 度数分布表で数字の範囲と階級数を決める際には、スタージェスの公式が使える。

