IRRとは、Internal Rate of Returnの略で、投資に対する収益率（利回り）を表します。
日本語では、内部収益率、内部利益率などと表現します。
IRRが10%のプロジェクトというのは、投資利回り10%のプロジェクトを意味します。
IRRを使うメリット
IRRを使うことで、プロジェクト間で収益化のタイミングが異なる場合でも、同じ指標でプロジェクトの収益率を議論できるようになります。
同じリターンであれば、早くリターンを得られるほどIRRは高くなります
（詳細は後ほどの事例で解説します）
IRRは、DCF法で投資判断をするときにNPVと並んでよく使われる判断指標です。
この記事では、このファイナンス理論の重要概念といえるIRRについて詳細を解説していきます。
IRRの計算方法は？
IRRは、その投資案件のNPVがゼロになる割引率として求められます。
たとえば、以下のような投資案件AとBを考えてみましょう。
| （万円） | 現在 | 1年目 | 2年目 | 3年目 | 4年目 |
| 投資案件A （設備投資） | -100 | 20 | 20 | 20 | 52 |
| 投資案件B （債券） | -100 | 3 | 3 | 3 | 103 |
投資案件A（設備投資）では、100万円を投資した後に、毎年20万円のキャッシュを回収でき、4年目のキャッシュ回収時点で設備を32万円で売却します。
投資案件A（設備投資）のIRRは、次のようになります。
投資案件AのIRR
-100 + 20／(1+r) ＋ 20／(1+r)2＋ 20／(1+r)3＋52／(1+r)4＝0
r = 3.98%
投資案件B（債券）では、同じく100万円を投資しますが、100万円を3％のクーポンの付いた債券に投資し、4年目の金利を得た時点で、元本を回収します。
投資案件B（債券）のIRRは、以下のとおりとなります。
投資案件AのIRR
-100 + 3／(1+r)＋3／(1+r)2＋3／(1+r)3＋103／(1+r)4 ＝ 0
r = 3%
この結果から、IRR（＝投資利回り）で見ると、投資案件Aの方が0.98％高いことがわかります。
IRRを使えばリターンの時間的価値も議論できる
投資案件AとBは、得られるキャッシュの総額である112万円だけに着目すると、どちらに投資しても優劣がないように見えます。
しかし、IRRを計算することで、リターンを早くリターンをもらえる投資案件Aの方が収益率がより優れた案件だと判断できました。
リターンの時間的価値は、DCF法の中で重要な概念ですが、IRRを使うことで時間的価値の優劣も判断できるようになるのです。
なお、投資案件AとBの割引率とNPVの関係をグラフで表すと、次のようになります。
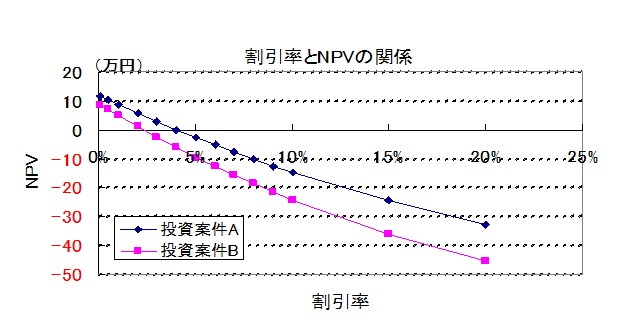
それぞれの曲線が、横軸（NPVが0の場所）と交わったときの割引率（横軸）の値がIRRです。
その他のIRRの事例は、以下の記事に載せているのであわせてご覧ください。
IRRはエクセルを使えば簡単に求められる
エクセルのIRR関数を使うと簡単にIRRを求められます。
IRR関数を使ってIRRを計算する
たとえば、1年目に-100の投資をして、2年目以降にリターンを得るというモデルを考えてみます。
| 1年目 | 2年目 | 3年目 | 4年目 | 5年目 |
| -100 | 40 | 35 | 40 | 55 |
この場合、IRR関数を使って、範囲として-100から55までの数字を一括して選択することで、IRRを求められます。
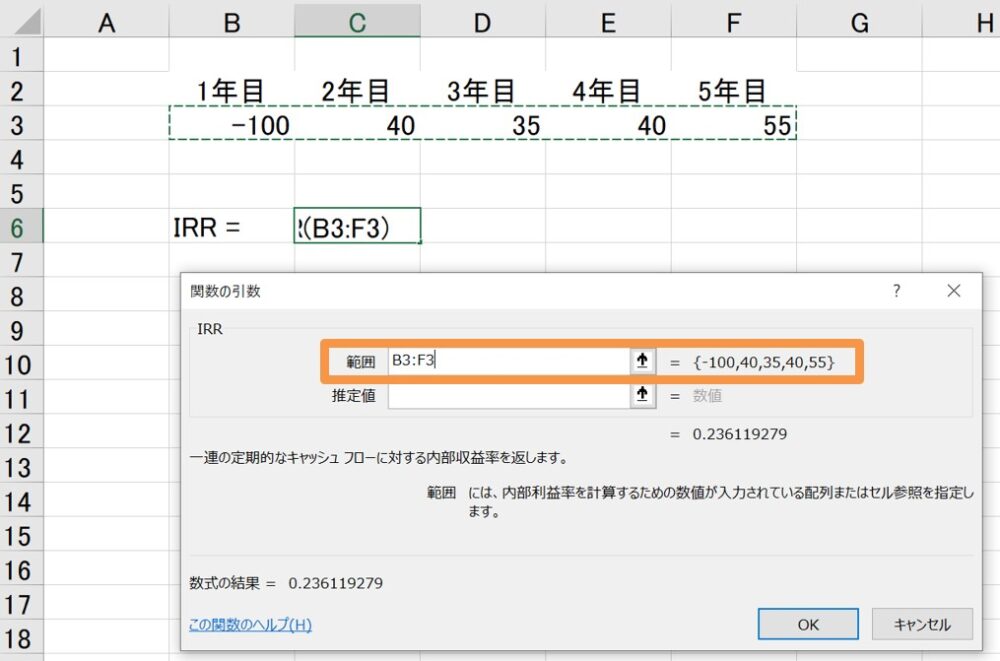
この例だと、IRRは24%になります。
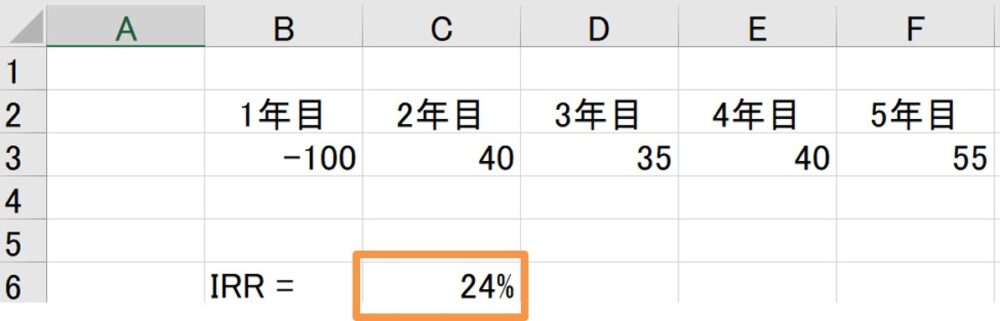
IRR関数を使うと、1セルごとの期間は自動的に1年になります。
複数のIRRが考えられる場合は、「推定値」に予め近い数字を入れておくことで、正しく計算できるようになります。（事例のような単純なケースでは、推定値は必要ありません）
XIRR関数を使ってIRRを計算する
IRR関数だと1年単位での利回り計算しかできませんが、XIRR関数を使うと利回りを日にち単位で分析できるようになります。
XIRR関数は、リターンの取得時期が一定間隔でない場合のIRR（内部収益率）を求める場合にも有効です。
たとえば、ある会社が次のような投資をしたとします。
- 2000年3月10日と7月6日に100万円ずつ投資する
- さらに2001年1月30日に200万円を投資する
- 2003年5月1日に600万円のリターンを得る
表にすると、以下のようになります。
| 2000/3/6 | 2000/7/8 | 2001/1/30 | 2003/5/1 |
| -100 | -100 | -200 | 600 |
この場合、次のようにXIRR関数を活用します。
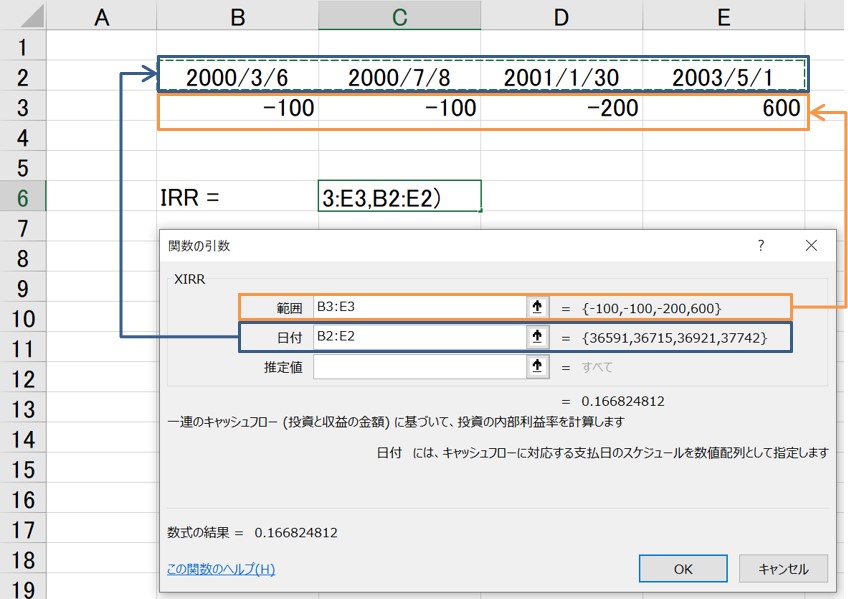
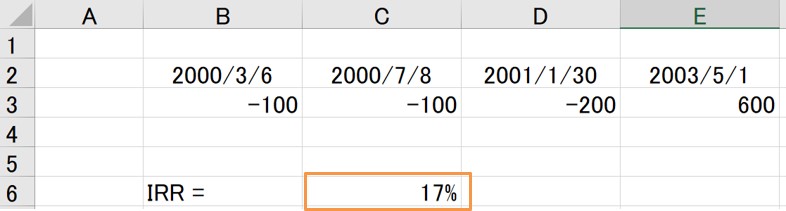
実際にXIRR関数を使って計算すると、IRRは17%と求められます。
IRRのデメリットは？
IRRには、次のようなデメリットがあります。
- IRRには利回りの観点しかないため、収益の規模を考慮できない。
- IRRは解が出ない場合がある。
プロジェクトを投資利回りの観点から議論できるので便利ですが、これらのデメリットには注意が必要です。
収益の規模を考慮できない
IRRは、あくまで収益率だけを求めるものなので、収益の規模を考慮に入れられません。
そのため、IRRを用いるときは、投資の前提条件に合わせて、NPVと併用して運用する必要があります。
一般的には、NPVとIRRのどちらを見るかの分かれ目として次のような考え方があります。
- 資金の制限が少なく、単一のプロジェクトを評価する場合は、NPVを重視して判断する。
- 限られた資金を複数の事業に分配することを考える場合は、IRRを重視して判断する。
IRRを用いるケースとNPVを用いるケースについて、詳細を以下の記事に記載しました。
IRRは解が出ない場合がある
②のIRRの解が出ない場合とは、下表のように期の途中にマイナスが出てしまう場合です。（期の途中にマイナスが出ると必ず解が出ないわけではありません）
(単位：万円）
| 現在 | 1年目 | 2年目 | 3年目 | 4年目 | |
| 例1 | -5 | 8 | 8 | 8 | -25 |
| 例2 | -15 | 8 | -5 | 5 | -5 |
これをグラフで視覚化すると次のようになります。
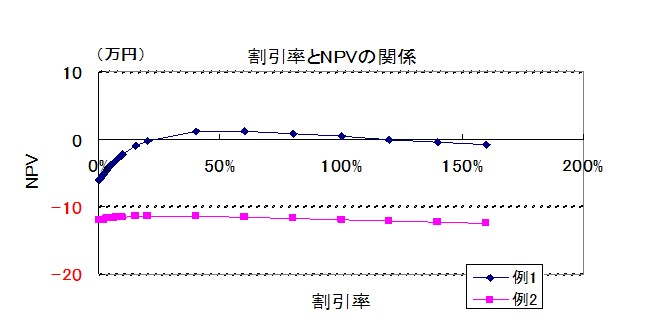
例1だと、グラフが横軸と2回交わっているので、IRRが2つ存在してしまいます。
例2だと、グラフが横軸と一度も交わらないので、IRRが存在しません。
まとめ
以上、IRRの解説でした。
- IRRとは、複利計算に基づいた、投資に対する収益率（利回り）のことで、NPVの累計がゼロになるときの割引率とも言い換えられる。
- IRRを使うことで、タイミングの異なる支出、収入に対する利回りを正確に求められる。
- エクセルのIRR関数を使えば、簡単にIRRを求められる。また、XIRR関数を活用することで、年単位に限らず、日にち単位での利回りを求めることもできる。
- 特に資本制約があり、限られた資源の中で、どの投資案件に投資をするかを判断する際に役立つ。
財務・ファイナンスをもっと知りたい方は
