標準偏差とは、データのバラツキの度合いを表す指標です。
標準偏差は、「各データが平均値から平均的に標準偏差の分だけ離れている」ことを表現していて、平均値100で標準偏差が20の場合、「平均値100に対して各データのばらつきの平均は20である」ことを表します。
標準偏差が大きいほどデータ同士のバラツキが大きく、標準偏差小さいほどデータ同士のバラツキが小さいことになります。
たとえば、左の図と右の図を比較すると、平均値は同じですが、バラツキ度合いが異なるのが見た目にもわかります。
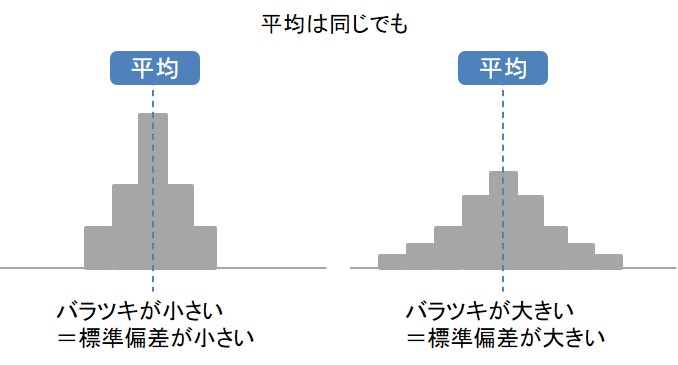 左図はバラツキ小さい=標準偏差が小さくなり、右図はバラツキが大きい=標準偏差が大きくなります。
左図はバラツキ小さい=標準偏差が小さくなり、右図はバラツキが大きい=標準偏差が大きくなります。
このように、平均値が同じであっても、母集団のバラツキ度合いによって標準偏差は変わってくるのです。
この記事では、その標準偏差の計算式・求め方、標準偏差とリスクとの関係などを解説していきます。
加えて、標準偏差と関係が深く、学力テストでよく使われている「偏差値」についても解説していきます。
標準偏差の求め方・計算式
標準偏差は、各データの値と平均値の差である「偏差」の2乗の総和となる「分散」の平方根をとったもので、「データの平均値を求める」「各データの偏差を求める」「偏差を2乗する」「分散を求める」「分散の平方根を計算する」という手順で求められます。
- データの平均値を求める:標準偏差を求めるためには、まずデータの平均値が必要です。データの合計をデータの個数で割ることで平均値を求めます。
- 各データの平均値からの偏差を求める:次に各データの平均値からの偏差を求めます。偏差とは各データから平均値を引いた差のことです。
- 各データの偏差を2乗する:上記で求めた偏差を2乗します。2乗をする理由は偏差の値が正負で打ち消さないようにするためです。
- 分散を求める:各データの2乗した偏差の平均を求めます。この2乗した偏差の平均のことを分散といいます。分散が大きければ大きいほどデータが上下に大きくばらついていることを表します。
- 分散の平方根を計算する:上記で求めた分散の平方根を求めることで、標準偏差を計算できます。
標準偏差を計算式で表現すると、以下のようになります。
標準偏差σ = 分散^(1/2)
分散 = ∑(各データの値 ー 母集団の平均値)^2 / データ数
※標準偏差はσ(シグマ)の記号で表されます
標準偏差の概念を図解で表現してみましょう。
たとえば、以下のように5つのデータがある場合、分散とは矢印の長さの2乗の総和のことになります。
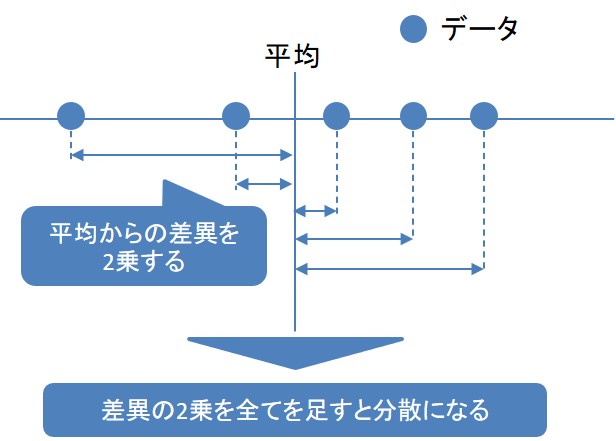
分散を求めるときに2乗しているのは、平均値との差をすべて正の値で表現するためです。
しかし、分散のままだと単位が元の単位の2乗のままになってしまうので、分散の平方根をとることで元データの単位とあわせられます。
その分散の平方根が「標準偏差」となり、データのバラツキ度合いを表す指標として使われているのです。
標準偏差の計算例
実際に標準偏差の計算例を見てみましょう。
母集団Aと母集団Bに、以下のようにそれぞれ10個のデータがあるとします。
| 母集団A | 5 | 6 | 4 | 3 | 2 | 5 | 4 | 3 | 5 | 4 | 平均4.1 |
| 母集団B | 9 | 2 | 10 | 3 | 1 | 4 | 2 | 7 | 2 | 1 | 平均4.1 |
どちらの母集団も、平均値は4.1で同じですが、一見すると母集団Bの方がバラツキが大きく見えます。
分散から標準偏差を求める方法
標準偏差の計算式に従って、まず母集団Aと母集団Bの分散を求めてみます。
母集団Aの分散
= (5-4.1)^2 + (6-4.1)^2 + (4-4.1)^2 +・・・+ (4-4.1)^2
= 1.43
母集団Bの分散
= (9-4.1)^2 + (2-4.1)^2 + (10-4.1)^2 +・・・+ (1-4.1)^2
= 11.21
上記の計算から求めた分散の平方根をとると、以下のように標準偏差を計算できます
母集団Aの標準偏差 = 1.43^(1/2) = 1.2
母集団Bの標準偏差 = 11.21^(1/2) = 3.3
このように標準偏差を求めることにより、数値的にも母集団Bの方がバラツキが大きいことが定量的にわかるようになります。
エクセルで標準偏差を求める方法
エクセルを使う場合は、「STDEV関数」を使うことで、標準偏差を一発で求めることができます。
エクセルを使って標準偏差を求める手順
- データを用意する:標準偏差を求めたいデータをエクセルのセルに入力します。
- STDEV関数を入力する:次にSTDEV関数を入力します。「=STDEV(データの範囲)」という形式にしてデータの範囲を指定します。
- 関数を適用する:STDEV関数の入力後にEnterキーを押して関数を適用することで、計算結果として標準偏差が表示されます。
先ほどの例でみると、母集団Aの場合、以下表の一番左の数値5から一番右の数値4のところをSTDEV関数で選択すれば簡単に求められます。
| 母集団A | 5 | 6 | 4 | 3 | 2 | 5 | 4 | 3 | 5 | 4 | 平均4.1 |
| 母集団B | 9 | 2 | 10 | 3 | 1 | 4 | 2 | 7 | 2 | 1 | 平均4.1 |
実際にSTDEV関数を使って標準偏差を求めているのが、以下の画面です。

STDEV関数さえ知っていれば、分散をわざわざ求めなくても、ほんの数秒で標準偏差を計算できます。
標準偏差のビジネスにおける使い方:事例
標準偏差のビジネスでの活用事例を2つ紹介します。
品質管理をするとき
ある母集団が、平均値を頂点とした理想的な分布(正規分布)をしていると仮定した場合、標準偏差σは次のような意味を持ちます。
- 平均値±1σの間に全データの68.27%が分布している。
- 平均値±2σの間に全データの95.45%が分布している。
- 平均値±3σの間に全データの99.73%が分布している。
- 平均値±6σの間に全データの99.999997%が分布している。
これを正規分布表を使って表すと、以下のようになります。
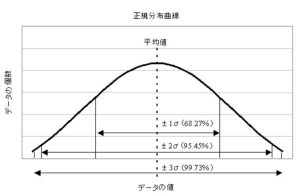
この考え方は、品質管理で応用されていて、品質管理では特に±3σが使われます。
たとえば、ある部品の寸法が100mmで、その設計上の許容差が±0.5mmだとして、部品を母集団から300個抜き取って、寸法を計測した結果、標準偏差σが0.1mmだとします。
規格上の許容差:±0.5mm
±3σ:±0.3mm
この結果を見ると、部品の寸法がバラついて3σになっても、許容差の範囲内に入っているので、想定外の製造上のバラツキが起きても十分な余裕があると言えます。
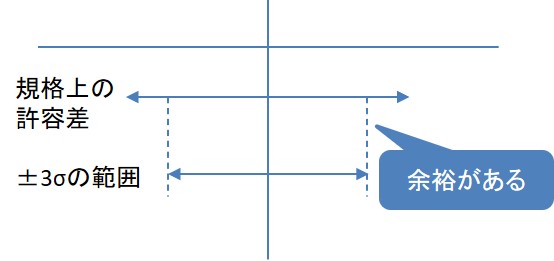
(この事例のように、許容差と標準偏差から製造工程の能力的な余裕を示す指標を工程能力指数と言います。詳細を知りたい場合は、工程能力指数で検索してください。)
このように標準偏差は、品質管理をする上で重要な指標として製造現場で活用されているのです。
他にも、経営改善にも使われるシックスシグマ(6σ)のシグマも元は標準偏差・バラツキからきていて、正常な範囲を6σまで許容できるとエラーが起きる確率が100万分の3や4まで下げられるところからシックスシグマと名付けられています。

リスクを定量的に評価するとき
ビジネスにおける定量分析の世界では、標準偏差のことをリスクといいます。
つまり、「リスクが大きい=バラツキが大きい」ということになります。
たとえば、次のように将来3パターンのシナリオに分かれる投資機会Aがあるとします。
投資機会A
| パターン | 収益 | 確率 |
| シナリオA | 100万円 | 20% |
| シナリオB | 50万円 | 60% |
| シナリオC | 5万円 | 20% |
このとき、収益の期待値は次のようになります。
期待値 = 100万×0.2 + 50万×0.6 + 5万×0.2 = 51万円
ここから標準偏差を求めるには、まず分散(標準偏差の2乗)を求めます。
分散
= (100万-51万)2×0.2 + (50万-51万)2×0.6 + (5万-51万)2×0.2
= 904万円2
分散の平方根をとると標準偏差は、以下のようになります。
標準偏差 = 約30万円
これを期待値が同じ51万円になるような次の投資機会Bと比べてみます。
投資機会B
| パターン | 収益 | 確率 |
| シナリオA | 71万 | 50% |
| シナリオB | 31万 | 50% |
期待値が同じなので、投資機会Aでも投資機会Bでも、どちらに投資してもよさそうに見えますが、リスクの観点から比較してみると異なる結果になります。
投資機会Bの標準偏差を投資機会Aと同じように計算すると、以下のようになります。
標準偏差 = 約20万円
つまり、投資機会Aと投資機会Bは全く期待値は同じですが、投資機会Bの方がよりリスクの低い投資だということがわかります。
このように標準偏差は、リターンに対するリスク分析としても活用できるのです。
標準偏差を活用した偏差値とは
標準偏差を使った指標のひとつとして、学力テストで出てくる偏差値があります。
偏差値とは、簡単に言うと、母集団の中で自分がどの程度の順位に位置しているかを示したものです。
偏差値の意味合い
仮に試験の点数が正規分布に従って分布している場合、偏差値と順位には次のような関係があります。
| 偏差値 | 上位からの% |
| 75 | 0.62% |
| 70 | 2.28% |
| 65 | 6.68% |
| 60 | 15.87% |
| 55 | 30.85% |
| 50 | 50.00% |
| 45 | 69.15% |
| 40 | 74.13% |
| 35 | 93.32% |
たとえば、試験を受験した人が10,000人いるとすると、偏差値70だと上位から228人に位置していることになり、偏差値65だと上位から668人に位置していることになります。
しかし、実際のテストの点数が完全な正規分布になることはまずないので、偏差値と順位の関係はあくまで目安として考える必要があります。
偏差値の求め方-エクセルで簡単に求められる
テストの点数の偏差値は、以下のように計算できます。
(テストの点数 - テストの平均点) ÷ 標準偏差 × 10 + 50
計算式を見てわかるように、テストの点数が平均点と同じであれば、偏差値は50になります。
たとえば、あるテストの分布が、以下のようになっていたとします。
| 生徒 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 母集団 | 70 | 81 | 66 | 54 | 90 | 49 | 67 | 78 | 77 | 55 | 68.7 |
このとき、エクセルのSTDEV関数を使って標準偏差を求めると、13.18になります。
標準偏差13.18と、上記の偏差値の式から、生徒A~Jの偏差値は次のように計算できます。
| 生徒 | A | B | C | D | E | F | G | H | I | J | 平均 |
| 母集団 | 70 | 81 | 66 | 54 | 90 | 49 | 67 | 78 | 77 | 55 | 68.7 |
| 偏差値 | 51.0 | 59.3 | 48.0 | 38.8 | 66.2 | 35.1 | 48.7 | 57.1 | 56.3 | 39.6 | – |
まとめ
以上、標準偏差の解説でした。
- 標準偏差とは、母集団の中にあるデータのバラツキを示したものである。
- 標準偏差は分散の平方根として求められる。分散は各データと平均値の差を2乗したものの総和である。
- 標準偏差はエクセルのSTDEV関数を使うと、簡単に計算できる。
- データが正規分布していると仮定すると、標準偏差を使うことで製造工程の信頼性を定量的に表すことができるので、標準偏差は品質管理によく応用されている。
- 定量分析においては、標準偏差をリスクと考えることもできる。たとえば、同じ期待値の投資機会であっても、標準偏差によってリスクの度合いを定量化できる。
- 学力テストで使われる偏差値も標準偏差を活用して求められる指標である。

